[프로그래머스] 프로그래머스 코딩테스트 고득점 Kit - 완전탐색 편
 오늘 포스팅은 완전탐색입니다.
오늘 포스팅은 완전탐색입니다.
피로도, 전력망을 둘로 나누기, 모음사전만 풀어보도록 합시다.
완전탐색을 위해서는 모든 경우의 수를 확인해야하는 경우가 있습니다. 간단하게는 모든 수들의 순열을 구해서 하는경우가 많은데
여기서 이전 순열 구하기 포스팅인 next_permutation을 많이 사용했습니다.
피로도
https://school.programmers.co.kr/learn/courses/30/lessons/87946

현재 피로도가 주어졌을 때 탐험할 수 있는 최대 던전 수를 구하는 문제입니다.
던전의 개수는 최대 8개이므로 완전탐색을 해도 괜찮을 정도이죠
순열로 구하기
단순히 던전의 모든 순열을 구해서 그 순서대로 던전을 몇 번 탐험할 수 있는지 계산하는 겁니다.
던전의 모든 순열을 구하는 법은 c++의 next_permutation을 사용하면 간단하게 구할 수 있죠
각 던전의 순열을 돌면서 피로도를 계산합니다. 만약 필요 피로도보다 현재 피로도가 작다면 continue를 해주면 되겠죠
반복되는 부분이 있을수도 있지만 입력의 크기가 작으므로 신경쓰지 않아도 됩니다.
코드로 바로 보시죠
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(int k, vector<vector<int>> dungeons) {
int answer = -1;
vector<int> per;
for (int i = 0; i < dungeons.size(); i++)
per.push_back(i);
do {
int count = 0;
int tempK = k;
for (int i = 0; i < per.size(); i++)
{
if (tempK >= dungeons[per[i]][0])
{
count++;
tempK -= dungeons[per[i]][1];
}
}
answer = max(answer, count);
} while (next_permutation(per.begin(), per.end()));
return answer;
}
서로 다른 던전이지만 피로도가 같을 수도 있습니다. 따라서 순열의 형태로 만들기 위해 인덱스 오름차순인 vector을 사용해서 순열을 만드는 겁니다.
dfs로 구하기
dfs를 사용해서도 문제를 풀 수 있습니다. 이래저래 순열을 구하는 것과 비슷하지만 계산은 조금 덜 한다고 생각합니다.
입출력 예로 설명해 봅시다.
피로도는 80이고 던전의 피로도 정보는 (80, 20), (50, 40), (30, 10) 입니다.
이를 현재 피로도가 최소 피로도보다 적거나 모든 던전을 다 돌때까지 dfs를 반복합니다.
(80, 0) // 현재 피로도와, 던전을 돈 횟수입니다.
| \ \
(60, 1) (40, 1) (70, 1) // 각 던전을 돌고 남은 피로도와, 던전을 돈 횟수를 갱신합니다.
|
(x) (20, 2) (50, 2) ... // 전에 이미 돈 던전이라면 무시합니다.
|
(10, 3) // 현재 피로도가 탐험할 던전의 최소 피로도보다 적으면 무시합니다.
// 이렇게 반복하며 나온 던전을 돈 횟수의 최대값을 반환하면 됩니다.
이를 코드로 나타내봅시다. 재귀함수의 인자로는 던전의 정보, 현재 피로도, 방문기록, 돈 횟수가 필요해보입니다.
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int maxCount = -1;
void dfs(vector<vector<int>> dungeons, int fatigue, vector<bool> checked, int count = 0)
{
maxCount = max(maxCount, count);
if (count == dungeons.size())
return;
for (int i = 0; i < dungeons.size(); i++)
{
if (checked[i] || fatigue < dungeons[i][0])
continue;
checked[i] = true;
dfs(dungeons, fatigue - dungeons[i][1], checked, count + 1);
checked[i] = false;
}
return;
}
int solution(int k, vector<vector<int>> dungeons) {
vector<bool> v(dungeons.size());
dfs(dungeons, k, v);
return maxCount;
}
정돈되지 않은 코드이지만 그래도 정답입니다!!
전력망을 둘로 나누기
https://school.programmers.co.kr/learn/courses/30/lessons/86971

트리형대의 전선의 간선을 하나 끊었을 때 최대한 노드의 개수가 비슷하게 맞추는 문제입니다.
즉 간선을 하나 끊었을 때의 두 트리의 노드 수의 차이가 가장 작은 수를 반환하면 됩니다.
여기서 다행히 전선이 사이클이 없는 트리형태이고 노드의 수는 최대 100개입니다.
즉 간선을 하나하나 끊어서 검사할 수 있는 완전탐색 문제입니다.
n wires result
9 [[1,3],[2,3],[3,4],[4,5],[4,6],[4,7],[7,8],[7,9]] 3
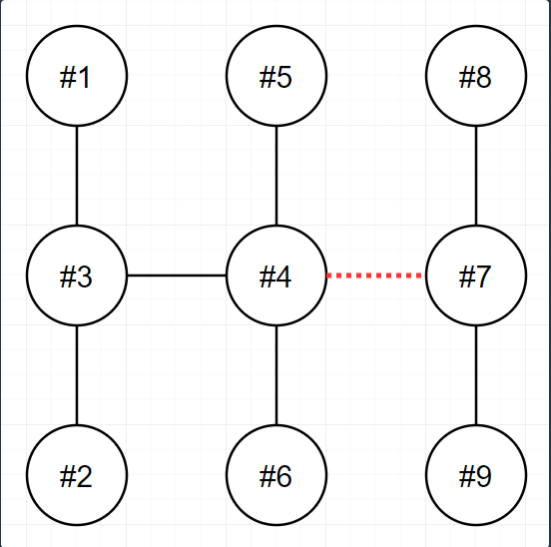
다음 예제를 살펴봅시다.
4와 7의 간선을 끊었을 때 dfs로 4번 노드에서 출발한 트리의 노드 수와 7번 노드에서 출발한 트리의 노드 수를 구하여
차이를 구하면 됩니다.
하지만 여기서 총 트리의 노드 수는 n이기 때문에 4번 노드에서 출발한 트리의 노드 수만 구하면 됩니다.
그럼 7번 노드에서 출발한 트리의 노드 수는 dfs를 하지 않아도
n - 4번 노드 트리의 노드 수
가 됩니다.
그리고 트리의 경우 사이클이 없기 때문에 중복체크를 매우 쉽게 할 수 있습니다.
단지 현재의 다음 노드가 현재의 이전 노드만 체크하면 됩니다.
각 간선의 배열은 wires로 주어지기 때문에 반복문을 돌면서 간선을 하나씩 끊으며 구하면 됩니다.
코드는 다음과 같습니다.
#include <string>
#include <vector>
#include <algorithm>
#include <math.h>
using namespace std;
vector<vector<int>> graph(200);
int dfs(int current, int exceptNode, int count = 1)
{
for (int i = 0; i < graph[current].size(); i++)
{
int next = graph[current][i];
if (next == exceptNode)
continue;
count = dfs(next, current, count + 1);
}
return count;
}
int solution(int n, vector<vector<int>> wires) {
int answer = 200;
for (int i = 0; i < wires.size(); i++)
{
graph[wires[i][0]].push_back(wires[i][1]);
graph[wires[i][1]].push_back(wires[i][0]);
}
for (int i = 0; i < wires.size(); i++)
{
int firstCount = dfs(wires[i][0], wires[i][1]);
int secondCount = n - firstCount;
answer = min(answer, abs(firstCount - secondCount));
}
return answer;
}
노드의 수는 최대 100개 입니다. 따라서 차이는 최대 99이지만 적당히 200으로 잡았습니다.
간선을 끊어주는 작업은 반복문을 돌면서 실제로 그래프를 새로 만들거나 끊는 작업은 비효율적입니다.
단지 끊긴 노드로 못가게만 하면 끊긴것과 다름이 없습니다. 따라서 dfs를 시작할 때 제일 처음으로 무시할 노드는
해당 노드와 인접한 끊긴 노드입니다. 그 다음은 앞서 말한대로 이전 노드가 될겁니다.
모음사전
https://school.programmers.co.kr/learn/courses/30/lessons/84512
A, E, I, O, U로만 사용하는 단어가 몇번째 단어인지 구하는 문제입니다.
고작 5개의 문자기때문에 모든 순서를 다 구해서 반복문을 통해 구하는 방법을 써도 됩니다.
정답처리도 문제없습니다.
하지만 그렇게 푸는건 조금 찝찝하니 규칙을 찾아봅시다.
AAAAA 로 시작되는 단어는 AAAAA 뿐입니다.
AAAA 로 시작되는 단어는 AAAA, AAAAA, AAAAE, AAAAI, AAAAO, AAAAU 6가지죠
여기서 뭔가 보입니다. 총 5가지 문자이므로 AAAA로 시작되는 단어는 AAAA자신과 AAAAA로 시작되는 단어 * 5이죠
AAA로 시작하는 단어 역시 AAA와 (AAAA 6개), (AAAE 6개), (AAAI 6개), (AAAO 6개), (AAAU 6개) 총 1 + 6 * 5 입니다.
이를 코드로 나타내봅시다.
vector<int> rule = { 0, 0, 0, 0, 1 }; // 5글자로 시작되는 단어는 5번째 값으로 생각하고 1로 설정합니다.
for(int i = 3; i >= 0; i++)
rule[i] = 1 + rule[i + 1] * 5; // 1 + 이전 개수 * 단어의 개수
정리해봅시다.
AAAAA => 1
AAAA => 6
AAA => 31
AA => 156
A => 781
입니다.
이 값을 토대로 계산해 봅시다. AAAE 는 몇번째 단어일까요??
우선 AAAA 로 시작되는 단어는 6개입니다. 그리고 A, AA, AAA각각 1개씩 있습니다. AAAA 다음은 AAAE이고요.
그럼 (1 + 1 + 1) + (6) + (1)로 10번째 입니다.
A, AA, AAA 1개씩 + AAAA로 시작되는 단어개수 + AAAA바로 다음 입니다.
I 도 해봅시다.
A로 시작되는 단어는 781개 입니다. 그럼 E로 시작되는 단어도 781개이고요. A로 시잗되는 단어와 E로 시작되는 단어
다음은 I가 되겠죠 그럼 781 + 781 + 1 로 1563이 됩니다.
EIO도 해봅시다.
A로 시작되는 단어는 781 입니다. 그 다음은 E이므로 781 + 1입니다.
AA로 시작되는 단어는 156 입니다. AE로 시작되는 단어도 156입니다. 그 다음은 AI가 됩니다. 따라서 156 + 156 + 1 입니다.
AAA로 시작되는 단어는 31, AAE도 31, AAI도 31, 그 다음은 AAO가 됩니다. 그럼 31 + 31 + 31 + 1 입니다.
이를 다 합치면 781 + 312 + 93 + 3 = 1189 가 됩니다.
그럼 코드로 짜봅시다!!
#include <string>
#include <vector>
#include <map>
using namespace std;
int solution(string word) {
int answer = 0;
vector<int> rule = { 0, 0, 0, 0, 1 };
string alpha = "AEIOU";
map<char, int> dict;
for (int i = 0; i < alpha.size(); i++)
dict[alpha[i]] = i;
for (int i = rule.size() - 2; i >= 0; i--)
rule[i] = 1 + rule[i + 1] * alpha.size();
for (int i = 0; i < word.size(); i++)
{
answer += dict[word[i]] * rule[i] + 1;
}
return answer;
}
앞서 설명한 내용을 그대로 코드에 적었습니다. 다만 AEIOU가 몇번째인지 알기 위해 map을 이용해 몇 번째인지 바로 알 수 있도록 했습니다.
규칙에 따라 값을 계산하니 알파벳 모음이 달라지지 않는다면 어떤 단어가 나와도 똑같은 시간이 걸릴것입니다.
느낀점
완전탐색문제인지 판별하기 위해서는 문제의 제약조건에서 입력의 크기를 유심히 봐야 합니다.
모든 경우의 수를 구해도 시간이 충분할것같다면 완전탐색으로 푸는것도 나쁘지 않습니다.
모든 경우의 수를 구해서 푼다는건 대체로 코드를 간단하고 빨리 짤 수 있으니까요.
모음사전의 문제같은 경우에도 처음에는 나오는 모든 단어를 미리 배열로 구해서 반복문으로 확인하는 식으로 풀었는데 5분도 걸리지 않았습니다.
만약 입력의 크기가 컸다면 이러한 방법은 무리였겠죠 그럴땐 규칙을 찾는 등 다른 방법을 생각해야 합니다.
Comments