[프로그래머스] 프로그래머스 코딩테스트 고득점 Kit - 동적계획법 편

오늘 포스팅할 내용은 동적계획법(Dynamic Programming) 입니다.

동적계획법은 불필요한 계산을 줄일 수 있어 잘 쓴다면 좋지만 어렵습니다…

난이도가 무려 3단계 3문제, 4단계 2문제로 총 5문제입니다.

난이도가 난이도인지라 이번에는 5문제 전부 포스팅해보겠습니다.

그래도 한번에 올리진 않고 나눠서 올려야 할것같네요.

이 포스팅에는 레벨3 3문제만 보겠습니다.

N으로 표현

https://school.programmers.co.kr/learn/courses/30/lessons/42895

한 자리 숫자와 사칙연산만으로 목표로 하는 숫자를 만드는데 가장 숫자를 적게 사용하여 만들어야 하는 문제입니다.
예시에는 덧셈과 나눗셈, 이어붙이기만 있는데 사칙연산이기에 뺄셈과 곱셈도 생각해줘야 합니다.

제한조건으로 최솟값이 8보다 크면 -1을 return하기에 숫자를 최대 8번 사용할 수 있습니다.

dfs로 무식하게 모든 경우의 수를 확인하며 풀어도 답은 됩니다.(제가 해봤어요…)
하지만 시간이 오래 걸리고 제한조건이 조금만 더 빡빡했다면 오답처리가 됐을겁니다.
따라서 좀 더 제대로 풀기 위해서는 dp를 활용하는게 좋습니다.

우선 숫자 하나로 표현할 수 있는 숫자는 자기자신밖에 없습니다.

그리고 숫자 2개로 표현할 수 있는 숫자는

1. 숫자하나 * 10 + 숫자하나
2. 숫자하나 + 숫자하나
3. 숫자하나 - 숫자하나
4. 숫자하나 * 숫자하나
5. 숫자하나 / 숫자하나 총 5가지입니다.
   

3개로 표현할 수 있는 숫자는 숫자 2개로 표현할 수 있는 숫자와 숫자 1개로 표현할 수 있는 숫자의 조합이겠죠.
여기서 중요한건 +, *는 두 피연산자의 순서를 바꿔도 똑같은 결과이지만 -, /는 바꾸면 다른 결과가 나옵니다.
따라서 3개로 표현할 수 있는 숫자는

1. 숫자 2개로 표현할 수 있는 숫자, 숫자 1개로 표현할 수 있는 숫자의 조합
2. 숫자 1개로 표현할 수 있는 숫자, 숫자 2개로 표현할 수 있는 숫자의 조합 입니다.
   

그럼 일반화를 해봅시다.
n개로 표현할 수 있는 숫자는
(n - 1, 1) (n - 2, 2) … (n - k, k) … (2, n - 2), (1, n - 1)
입니다.

조합으로 나온 결과가 중복된 값이 나올 수 있으니 Set 자료구조를 사용합시다.
그리고 최대 8개의 숫자로 표현할 수 있는 값을 넣어둘 크기가 9짜리 배열을 사용합시다. (0번째는 비워둠..)

그럼 코드는 다음과 같습니다.

#include <string>
#include <vector>
#include<iostream>
#include<set>

using namespace std;

set<int> dp[9];

int solution(int N, int number) {
    int answer = -1;

    int num = 0;
    for (int i = 1; i <= 8; i++)
    {
        num = num * 10 + N;
        dp[i].insert(num);
        for (int j = 1; j < i; j++)
        {
            for (auto iter = dp[j].begin(); iter != dp[j].end(); iter++)
            {
                for (auto innerIter = dp[i - j].begin(); innerIter != dp[i - j].end(); innerIter++)
                {
                    dp[i].insert(*iter + *innerIter);
                    dp[i].insert(*iter - *innerIter);
                    dp[i].insert(*iter * *innerIter);
                    if(*innerIter != 0)
                        dp[i].insert(*iter / *innerIter);
                }
            }
        }

        for (auto iter = dp[i].begin(); iter != dp[i].end(); iter++)
            if (*iter == number)
                return i;
    }
    return answer;
}

dfs로 풀었던 코드의 결과가 없어져서 정확한 비교는 못하지만 기억상으로 비교하자면 어떤 케이스는 1000배 시간차이가 나기도 하는군요…
동적계획법 만만세입니다.

시간복잡도의 경우에는 8번 반복이 전제이기 때문에 O(1)이라고 생각합니다.
하지만 제한조건이 걸려있지 않았다면 한번 진행할 때마다 기하급수적으로 늘어나기 때문에 와우우우…
계산하기가 쉽지 않네요…

정수 삼각형

https://school.programmers.co.kr/learn/courses/30/lessons/43105?language=cpp

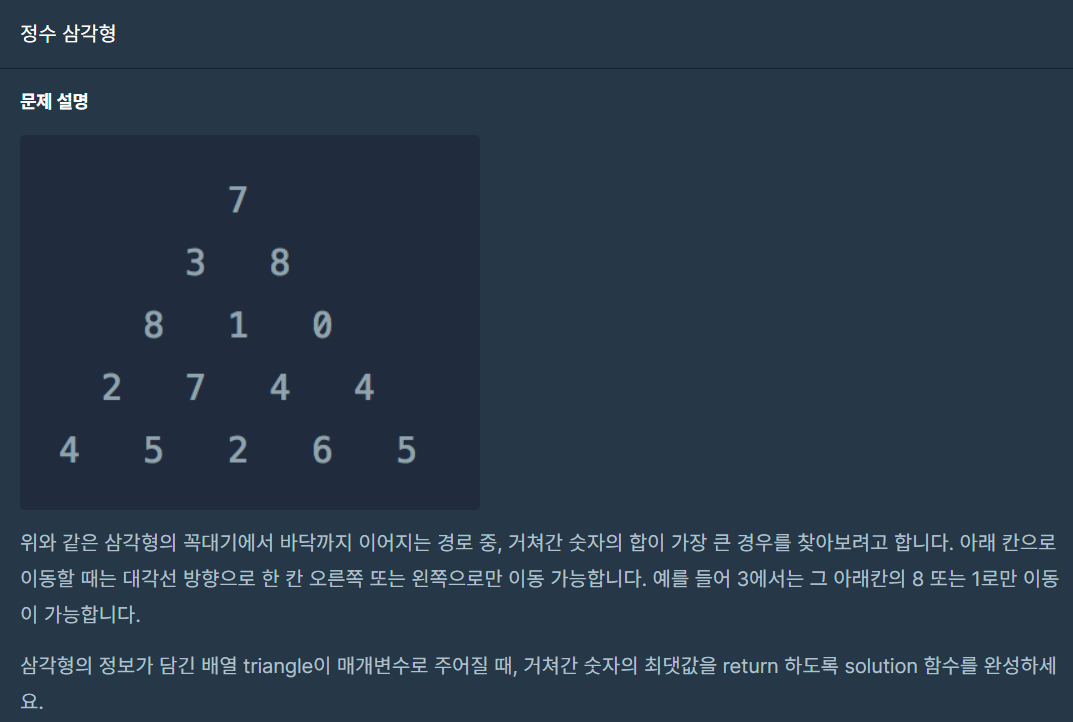
동적계획법 문제치고는 쉬운 편입니다.

삼각형 제일 위에서 제일 밑으로 내려오면서 거쳐간 숫자의 합이 가장 큰 경우를 찾으면 되는 문제입니다.

2차원 배열을 만들어 삼각형을 내려올 때마다 어떤 값을 더해야 더 큰지 판단하고 더한 값을 저장하면서 내려와 가장 밑에 숫자들 중 최댓값을 찾아 반환하면 됩니다.

이동할 때는 대각선 방향으로 한 칸씩만 이동할 수 있습니다.

삼각형의 특성상 각 단계에서 제일 오른쪽과 왼쪽은 그대로 내려오는 수밖에 없습니다.

그리고 사이의 값들은 오른쪽 대각선, 왼쪽 대각선 중 큰값을 더해서 저장해야 합니다.

따로 뭐 설명할게 없네요…
코드로 확인합시다!!

#include<iostream>
#include <string>
#include <vector>

using namespace std;

int solution(vector<vector<int>> triangle) {
    int answer = 0;

    // dp 생성
    vector<vector<int>> dp(triangle.size());

    // dp 초기화
    for (int i = 0; i < triangle.size(); i++)
    {
        dp[i] = vector<int>(triangle[i].size());
    }

    // 맨 위의 최댓값은 삼각형의 최댓값
    dp[0][0] = triangle[0][0];

    for (int i = 1; i < triangle.size(); i++)
    {
        // 제일 오른쪽과 왼쪽은 그대로 내려오는 수밖에 없음
        dp[i][0] = triangle[i][0] + dp[i - 1][0];
        dp[i][triangle[i].size() - 1] = triangle[i][triangle[i].size() - 1] + dp[i - 1][triangle[i - 1].size() - 1];

        // 사이에 있는 곳들은 오른쪽 대각선과 왼쪽 대각선의 값중 큰 값과 더해서 저장됨
        for (int j = 1; j < triangle[i].size() - 1; j++)
        {
            dp[i][j] = max(triangle[i][j] + dp[i - 1][j - 1], triangle[i][j] + dp[i - 1][j]);
        }
    }

    // 맨 밑에 값들 중 최댓값이 정답!
    for (int i = 0; i < dp[dp.size() - 1].size(); i++)
        answer = max(answer, dp[dp.size() - 1][i]);

    return answer;
}

3단계치고는 쉬운 문제였습니다.
모든 경로를 확인하는 것이 아닌 dp를 활용하여 기존의 경로의 값을 사용하기 때문에 시간복잡도는 O(N^2)으로 풀 수 있었습니다.

등굣길

https://school.programmers.co.kr/learn/courses/30/lessons/42898?language=cpp

오른쪽과 아래쪽으로만 움직여 집에서 학교가 있는 곳까지 최단경로의 개수를 구하는 문제입니다.
다만 물에 잠긴 지역은 이동할 수 없어 이 부분을 생각해줘야 합니다.
또 경우의 수가 많기 때문에 1,000,000,007로 나눈 나머지를 return해야 합니다.

집의 좌표는 (1, 1)이고 학교의 좌표는 (m, n)입니다.
그리고 오른쪽과 아래쪽으로만 이동할 수 있기에 물웅덩이만 피하면 어떤 경로든 최단경로가 될 수 밖에 없습니다.

2차원 배열을 이용해 해당 좌표로 가는 최단경로의 개수를 dp로 삼고 계속 진행하여 (m, n)좌표에 도달했을 때 계산된 값을 return하면 되겠죠.
계산하는 방법은 단순합니다.
해당좌표의 최단경로 개수는 해당좌표 위쪽의 최단경로 개수 + 해당죄표 왼쪽의 최단경로 개수 입니다.
일반화해보면
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 입니다.

물웅덩이의 dp값은 당연히 0으로 해줘야 합니다.

코드는 다음과 같습니다.

#include <string>
#include<iostream>
#include <vector>

#define MOD 1000000007

using namespace std;

int solution(int m, int n, vector<vector<int>> puddles) {
    int answer = 0;
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));

    // 물웅덩이 좌표 초기화
    for (auto p : puddles) dp[p[0]][p[1]] = -1;

    // 시작점 초기화
    dp[1][1] = 1;

    // 좌표를 돌면서 계산해줌
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (dp[i][j] == -1) dp[i][j] = 0;   // 물웅덩이라면 0으로 해줌
            else dp[i][j] += (dp[i - 1][j] + dp[i][j - 1]) % MOD;  // 위 좌표, 오른쪽 좌표의 dp값을 더해주고 나누라고 한 값으로 나눈 나머지를 넣어준다.
        }
    }

    return answer = dp[m][n];
}

이 문제도 레벨3 치고는 쉬웠습니다.
시간복잡도는 좌표를 도는 부분이 있어 O(MN)이 되겠습니다.

느낀 점

동적계획법은 어려우면 진짜 어렵게 낼 수 있습니다. 이 정도 문제라 다행이였습니다.
동적계획법의 어려운 점은 어떤걸 dp로 만들것인가? 점화식의 형태는 어떤식인가를 생각해야하기 때문에 어렵습니다.
물론 동적계획법 문제를 많이 풀다보면 쉬운 문제는 단번에 이런 점화식 형태를 쓰면 되겠다 생각이 난답니다.
즉 동젹계획법 역시 잘 풀려면 많은 문제를 풀어야 합니다….
다음 포스팅은 이번에 다루지 않았던 레벨4 2문제를 다뤄보겠습니다.