[항해99 코테 스터디] 7일차 문제

오늘도 항해 99 코테 스터디 3번째 TIL입니다.
11월 2일의 미들러 문제와, 11월 3일의 첼린저문제를 풀어봤습니다.
모음사전
https://school.programmers.co.kr/learn/courses/30/lessons/84512
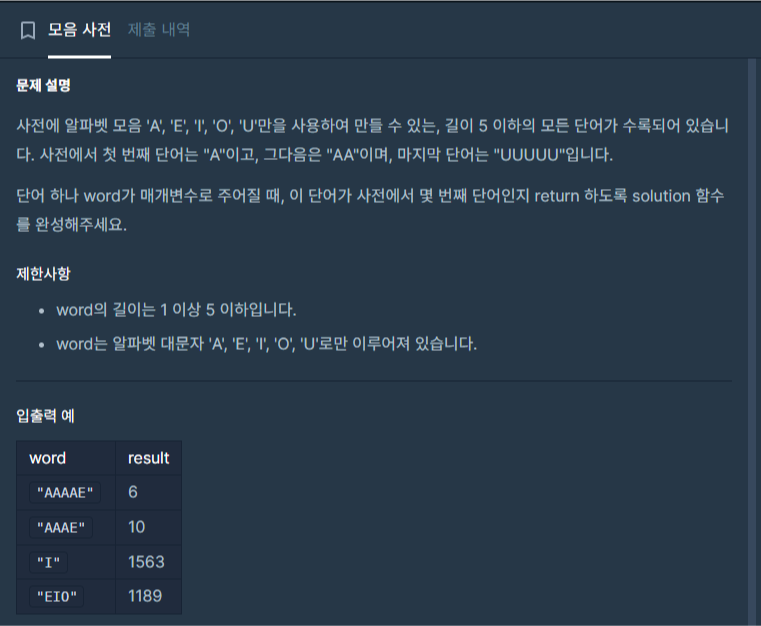
이전에 풀어본 문제인데다가 블로그에 포스팅도 해놨습니다.
풀이과정은 똑같으므로 설명은 이전 포스팅을 참조하겠습니다.
https://hyeonjunje.github.io/codingtest/ProgrammersExhaustiveSearch/#%EB%AA%A8%EC%9D%8C%EC%82%AC%EC%A0%84
이번에 푼 문제의 코드입니다.
#include <string>
#include <vector>
#include <map>
#include<iostream>
using namespace std;
int solution(string word) {
int answer = 0;
string alpha = "AEIOU";
map<char, int> m;
int digitNumber[5];
digitNumber[4] = 1;
for(int i = 3; i >= 0; --i)
{
digitNumber[i] = digitNumber[i + 1] * 5 + 1;
}
for(int i = 0;i < alpha.size(); ++i)
{
m[alpha[i]] = i;
}
for(int i = 0; i < word.size(); ++i)
{
char ch = word[i];
answer += (1 + m[ch] * digitNumber[i]);
}
return answer;
}
키 순서
https://www.acmicpc.net/problem/2458

딱 문제를 보면 정점이 500으로 굉장히 작습니다.
그래서 막 풀면 될 줄 알고 dfs를 여러번해서 각 정점에 연결된 노드를 저장한다음
모든 dfs가 끝났을 때 정점을 돌면서 다 연결되어있는 정점이라면 count를 1씩 증가시켜줘서 답을 찾을려고 했습니다.
그래서 나온 코드가
#include<iostream>
#include<vector>
#include<set>
#define MAX 501
using namespace std;
set<int> d[MAX];
vector<int> graph[MAX];
bool visited[MAX] = { false, };
void dfs(int start)
{
visited[start] = true;
for (int i = 0; i < graph[start].size(); ++i)
{
int next = graph[start][i];
if (!visited[next])
{
for (auto it = d[start].begin(); it != d[start].end(); ++it)
{
d[next].insert(*it);
}
dfs(next);
}
}
}
void dfs2(int init, int start)
{
visited[start] = true;
d[init].insert(start);
for (int i = 0; i < graph[start].size(); ++i)
{
int next = graph[start][i];
if (!visited[next])
{
dfs2(init, next);
}
}
}
void Init(int n)
{
for (int i = 1; i <= n; ++i)
{
visited[i] = false;
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n, m, a, b;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
d[i].insert(i);
}
for (int i = 0; i < m; ++i)
{
cin >> a >> b;
graph[a].push_back(b);
}
for (int i = 1; i <= n; ++i)
{
Init(n);
dfs(i);
}
for (int i = 1; i <= n; ++i)
{
Init(n);
dfs2(i, i);
}
int result = 0;
int answer = 0;
for (int i = 1; i <= n; ++i)
{
answer += i;
}
for (int i = 1; i <= n; ++i)
{
int temp = 0;
for (int val : d[i])
{
temp += val;
}
if (temp == answer)
{
result++;
}
}
cout << result;
}
테스트케이스는 올바른 답을 반환했지만 제출결과는 시간 초과였습니다.
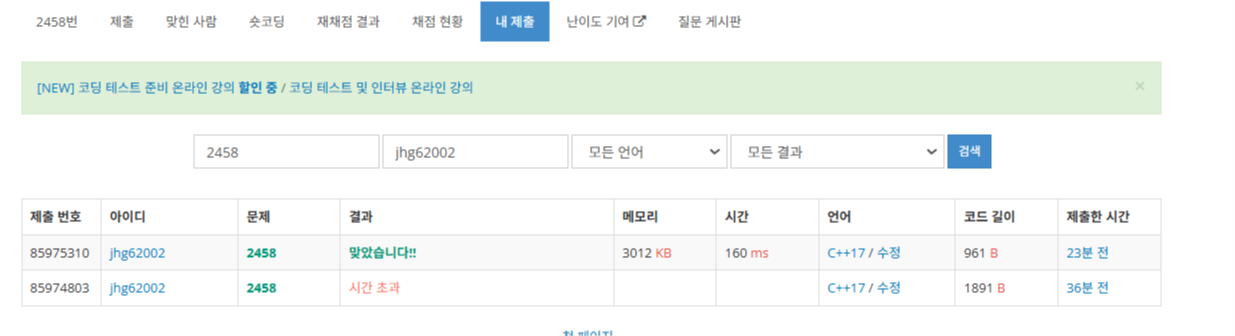
그래서 처음부터 잘못된걸 깨닫고 다시 문제를 읽어봤습니다.
입력 정보를 잘 보면 정점보다 간선의 개수가 훨씬 많습니다. 여기서 무작정 플로이드 와샬 알고리즘이 떠올랐습니다.
모든 정점끼리의 거리를 구합니다. 각 정점마다 거리는 1로 둡니다.
만약 다 모든 정점이 다 이어져있어 정점마다의 거리를 저장한 배열이 다 갱신되어있으면 키를 정확하게 알 수 있겠죠
예를 들어 4번 정점이라면
4 -> 1 거리 : INF
4 -> 2 거리 : 1
4 -> 3 거리 : INF
4 -> 4 거리 : 0
4 -> 5 거리 : INF
4 -> 6 거리 : 1
입니다. 방향그래프이다 보니 반대로는 갈 수 없어 그림에선 다 이어져있지만 무한대의 거리이죠
그럼 무한대일 경우에는 반대로 보면됩니다.
1 -> 4 거리 : 2
4 -> 2 거리 : 1
3 -> 4 거리 : 1
4 -> 4 거리 : 0
5 -> 4 거리 : 1
4 -> 6 거리 : 1
이러면 4는 모든 정점과 연결되어있다는것을 알 수 있습니다.
플로이드 와샬을 이용하면 쉽게 구현할 수 있겠죠
그럼 이를 적용시킨 코드는 다음과 같습니다.
#include<iostream>
#include<vector>
#define MAX 501
#define INF 1000000
using namespace std;
vector<int> graph[MAX];
int d[MAX][MAX];
void FloydWashal(int n)
{
for (int k = 1; k <= n; ++k)
{
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n, m, a, b;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
}
}
for (int i = 0; i < m; ++i)
{
cin >> a >> b;
d[a][b] = 1;
}
FloydWashal(n);
int answer = 0;
for (int i = 1; i <= n; ++i)
{
long long result = 0;
for (int j = 1; j <= n; ++j)
{
if (d[i][j] >= INF)
{
result += d[j][i];
}
else
{
result += d[i][j];
}
}
if (result < INF)
{
answer++;
}
}
cout << answer;
}
느낀 점
모음사전은 오랜만에 푸는데도 그때 인상깊어서 그런가 아직도 풀이방법이 기억이 났었네요
역시 문제를 많이 풀어봐야 좋은듯합니다.
키 순서 문제는 뻘짓을 많이 해서 시간이 좀 걸렸는데 플로이드 와샬을 알아차리니까 푸는데는 시간이
얼마 걸리지 않았습니다.
늘 생각하지만 입출력의 크기 제한을 제대로 봐야한다는걸 또다시 깨달았습니다.
Comments