[C++ / Algorithm] MST(Minimum Spanning Tree, 최소 신장 트리)

알고리즘 문제에서 다양하게 나올 수 있는 알고리즘입니다.
가중치 그래프에서 비용이 제일 작게 나올 수 있는 그래프를 구할 때 사용할 수 있죠!!
따라서 이번 포스팅은 MST 입니다.

Spanning Tree (신장 트리)

최소 신장 트리를 알기 전에 신장 트리가 뭔지 알아야 합니다.

신장 트리는 그래프 내의 모든 정점을 포함하는 그래프의 부분집합입니다.
따라서 하나의 그래프에 여러개의 신장트리가 있는 형태입니다.


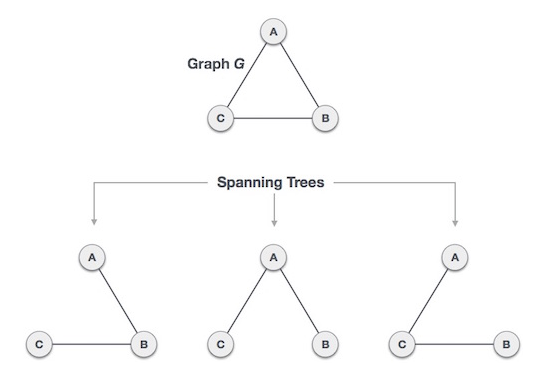
출처 : https://www.tutorialspoint.com/data_structures_algorithms/spanning_tree.htm

신장 트리의 특징은 다음과 같습니다.

1. 모든 정점을 포함한다.
2. 하나의 그래프에 복수개의 신장 트리가 존재할 수 있다.
3. cycle이 생기지 않는다.
   
   
   

Minimum Spanning Tree (최소 신장 트리)

신장 트리를 알았으니 최소 신장 트리는 이름 그대로 무언가 제일 최소인 신장 트리겠죠.
무언가 작다 크다를 판별할 수 있는건 가중치 그래프의 비용(가중치)입니다.

즉 어떤 그래프의 여러 신장 트리중 비용(가중치)이 제일 작은 트리를 최소 신장 트리 입니다.

최소 신장 트리를 구하는 데에는 2가지 알고리즘이 있습니다.

1. kruskal algorithm
2. prim algorithm
   
   

Kruskal Algorithm

Kruskal 알고리즘은 대표적인 greedy algorithm으로 비용이 제일 적은 간선부터 확인하면서 그래프를 연결합니다.
연결하면서 cycle이 생긴다면 연결을 하지 않고 진행합니다.
모든 간선을 다 확인할 때까지 반복을 하면 됩니다.

1. 간선들을 비용 오름차순으로 정렬한다.
2. 정렬된 모든 간선들을 하나씩 반복한다.
    cycle이 생기지 않으면 두 정점을 연결한다.

cycle을 확인하는 방법은 각 정점마다 부모 노드를 확인하여
연결할려는 두 정점의 부모가 같으면 cycle이 생긴것으로 판단하고 연결을 무시합니다.
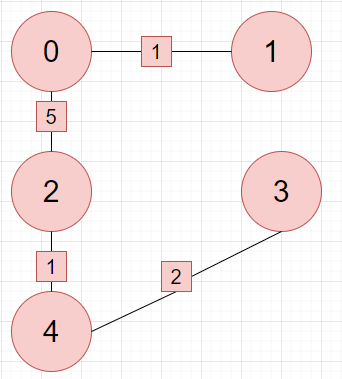
예제로 알아봅시다.

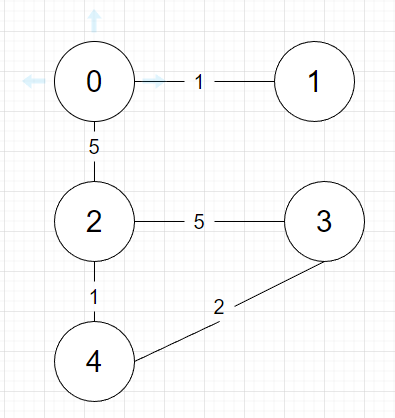
이런 그래프가 있다고 합시다.

그래프를 연결하기 전인 처음에는 각 노드들의 부모를 자기 자신으로 초기화를 합니다.
정점 0 1 2 3 4
부모 0 1 2 3 4

{시작 정점, 연결된 정점, 비용}의 형태를 가지는 간선들을 비용순으로 정렬하면 다음과 같습니다.
[[0, 1, 1], [2, 4, 1], [3, 4, 2], [0, 2, 5], [2, 3, 5]]
간선 순서대로 진행해봅시다.

1. {0, 1, 1}

0과 1의 부모가 같지 않으므로(cycle이 생기지 않으므로) 연결해줍니다.
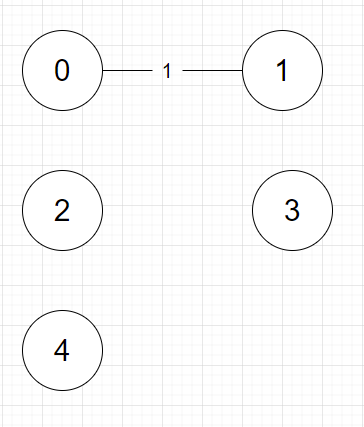
연결하면 부모는 다음과 같습니다.
정점 0 1 2 3 4
부모 0 0 2 3 4

1. {2, 4, 1} 2와 4의 부모가 같지 않으므로(cycle이 생기지 않으므로) 연결해줍니다.
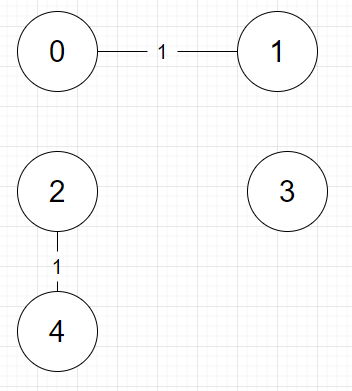
   연결하면 부모는 다음과 같습니다.
   정점 0 1 2 3 4
   부모 0 0 2 3 2
   

2. {3, 4, 2} 3과 4의 부모가 같지 않으므로(cycle이 생기지 않으므로) 연결해줍니다.
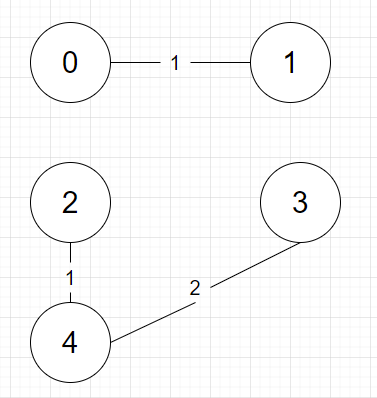
   연결하면 부모는 다음과 같습니다.
   정점 0 1 2 3 4
   부모 0 0 2 2 2
   

3. {0, 2, 5} 0과 2의 부모가 같지 않으므로(cycle이 생기지 않으므로) 연결해줍니다.
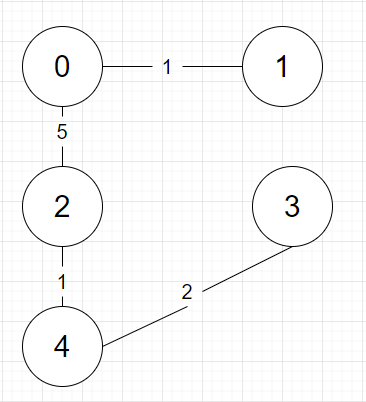
   연결하면 부모는 다음과 같습니다.
   정점 0 1 2 3 4
   부모 0 0 0 0 0
   

4. {2, 3, 5} 2와 3의 부모가 같으므로 연결하지 않습니다.
   

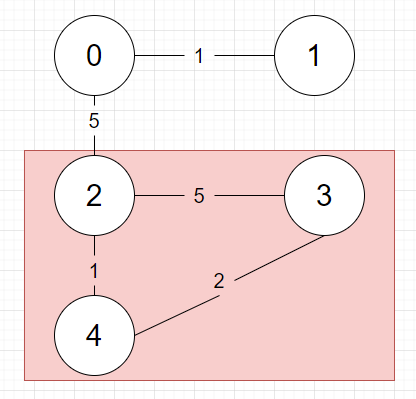
그럼

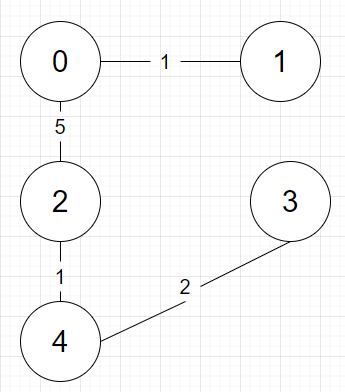
이런 최소 신장 트리가 완성됩니다.
총 길이는 연결해줄 때마다 더해주는 등 구할 수 있는 방법은 여럿 있습니다.

코드로 나타내면 다음과 같습니다.

#include<iostream>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> parent;

bool comp(vector<int> a, vector<int> b)
{
    return a[2] < b[2];
}

int findParent(int idx)
{
    if (parent[idx] == idx)
        return idx;
    return parent[idx] = findParent(parent[idx]);
}

// 정점의 개수와 간선의 정보를 받습니다.
int Kruskal(int n, vector<vector<int>> edges)
{
    int answer = 0;
    sort(edges.begin(), edges.end(), comp);
    for (int i = 0; i < n; i++)
        parent.push_back(i);

    for (int i = 0; i < edges.size(); i++)
    {
        int start = findParent(edges[i][0]);
        int end = findParent(edges[i][1]);
        int cost = edges[i][2];

        if (start != end)
        {
            answer += cost;
            parent[end] = start;
        }
    }
    return answer;
}

Prim Algorithm

Prim 알고리즘도 역시 greedy 알고리즘입니다.
다만 간선 비용의 최소를 무작정 찾는 Kruskal 알고리즘과 다른 방식의 greedy 알고리즘이죠

그래프의 임의의 정점을 선택하고 그 정점의 최소 간선을 구하여 트리로 만듭니다.
트리에 있는 모든 정점들의 최소 간선을 구하여 또 트리로 뻗어나갑니다.
이런 식으로 진행하여 모든 정점이 트리에 포함된다면 최소신장트리가 완성됩니다.

Prim 알고리즘도 그림으로 설명하겠습니다.

kruskal 알고리즘과 똑같은 그래프입니다.
이 그래프를 prim 알고리즘으로 최소신장트리를 만들어봅시다.
시작은 어느 곳에서 해도 됩니다. 저는 0에서 출발하겠습니다.

0에서 출발하기에 현재 트리는 정점 0 하나 입니다.

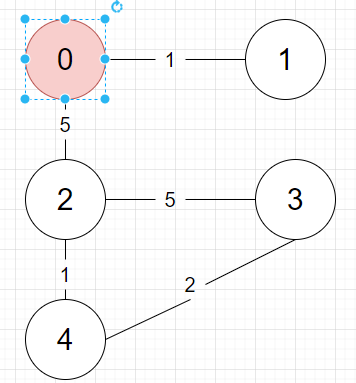
정점 0의 간선 중 최소는 정점 1과 이어지는 1입니다. 이어줍니다.

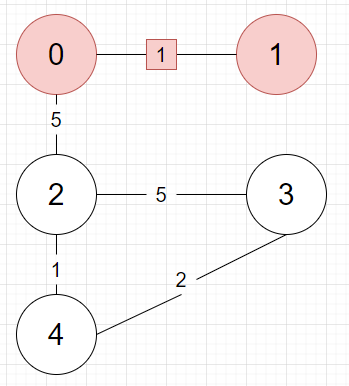
현재 트리의 정점 중 간선은 0과 2 사이의 5 뿐입니다. 이어줍니다.

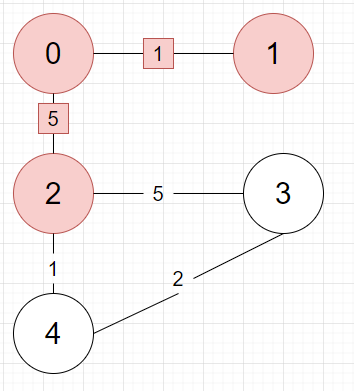
현재 트리의 간선들 중 최소는 2와 4 사이 1입니다. 이어줍시다.

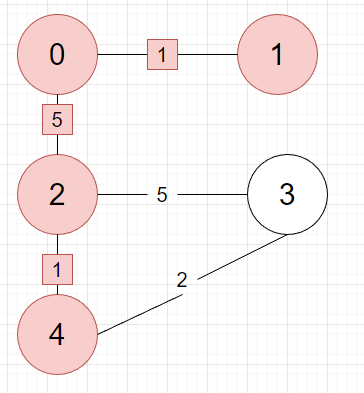
현재 트리의 간선들 중 최소는 3과 4 사이 2입니다. 이어줍시다.

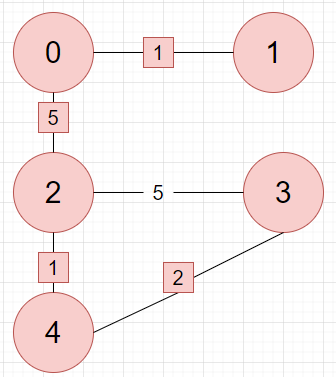
만든 트리에 모든 정점이 포함되었으니 최소신장트리가 완성됩니다.

현재 트리의 정점들의 간선중 최소를 구하는것은 최소힙을 사용하면 O(logn)으로 최솟값을 구할 수 있습니다.

코드로 나타내면 다음과 같습니다.

#include<iostream>
#include <vector>
#include <algorithm>
#include <queue>

using namespace std;

vector<pair<int, int>> graph[100];
bool visited[100];

struct cmp {
    bool operator()(pair<int, int> a, pair<int, int> b)
    {
        return a.second > b.second;
    }
};

int solution(int n, vector<vector<int>> costs) 
{
    int answer = 0;

    for (int i = 0; i < costs.size(); i++)
    {
        graph[costs[i][0]].push_back({ costs[i][1] , costs[i][2] });
        graph[costs[i][1]].push_back({ costs[i][0] , costs[i][2] });
    }

    priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pq;

    for (int i = 0; i < graph[0].size(); i++)
        pq.push(graph[0][i]);
    visited[0] = true;
    int cnt = 0;

    while (cnt < n - 1)
    {
        pair<int, int> cur = pq.top();
        pq.pop();

        int node = cur.first;
        int cost = cur.second;

        if (visited[node]) continue;

        answer += cost;
        visited[node] = true;
        cnt++;

        for (int i = 0; i < graph[node].size(); i++)
        {
            int next = graph[node][i].first;
            if (!visited[next])
                pq.push(graph[node][i]);
        }
    }
    return answer;
}

시간복잡도

정점 개수 : V, 간선 개수 : E

kruskal알고리즘은 정렬하는 부분이 다 합니다.
O(ElogE) 입니다.

prim 알고리즘은 각 노드마다 우선순위 큐를 뽑으니 O(VlogV) 입니다.
또 현재 노드의 간선을 돌면서(O(E)) 방문하지 않았다면 우선순위 큐에 집어넣는 동작(O(logV))을 합니다. 즉 O(ElogV)
그럼 O(VlogV) + O(ElogV)이고 대부분 정점보다 간선이 많으므로
O(ElogV) 입니다.

big-O notation이기 때문에 자세하게는 대강 계산된 시간복잡도입니다.
입력이 어마무시하게 많지 않은 이상 두 알고리즘 다 비슷비슷할겁니다.